Using Pyth To Seed A Random Number Generator

July 05 2022

In our previous post we compared a few different methods of generating random numbers on the Solana blockchain. The use case in that instance was strictly for programs that weren't using those random values for anything where real world value was at stake (i.e. not in a gambling app). As everything about the RNG sequence was transparent, it meant that it was easy for anyone to predict the next values, and therefore manipulate the system that used them.

In this post we are going to extend the previous functionality by generating the seed for out random number generator (RNG) using information from off-chain via the oracle Pyth. At time of writing Pyth provides free access to price data for around 80 different crypto and non-crypto assets, and adds very little computational cost to use within a program on-chain.

The advantage of doing this is that the entire process remains largely trustless (a user only needs to trust that Pyth isn't somehow manipulating the data being sent to the program to their advantage) and means that we can use our RNGs in a much wider range of applications. Although we wouldn't recommend using this for gambling apps where the outcome of a bet is generated within the same block as the bet is made, for applications where winners are selected some time after entries have closed this process can provide extremely good random values to seed our RNG. In general the security of the seed will increase as the time interval before selecting any winners increases, however any change to any of the price streams (including their provided confidence intervals) that we include in our seed generator will yield entirely independent values for the seed. As it is adds very little computational cost to include more streams in the creation of the seed, you could easily include dozens to increase security, though in this post we will build our seed using only three.

The code for the on-chain program described in this post can be found here and by the end we will have covered the following:

• Used Pyth to stream price data to our on-chain program
• Create a random seed using that data using techniques from our previous post
• Demonstrated the robust nature of the seeds generated

Using Pyth to stream price data on-chain

The rust crate required to use Pyth can be found here. In our example program we will be using price series data from three cryptocurrency streams: BTC, ETH and SOL. Pyth provide the public keys for each of their supported price streams (for example on the Solana devnet you can find them here) and these will need to be provided to your program when you interact with it in the list of accounts to be accessed.

Below we will go through the process of obtaining the current price and the provided confidence interval for the BTC case. The ETH and SOL cases can be found in the program source code, but just follow the same pattern.

    // in processor.rs 
    let account_info_iter = &mut accounts.iter();
    let BTC_key = Pubkey::from_str("HovQMDrbAgAYPCmHVSrezcSmkMtXSSUsLDFANExrZh2J").unwrap();

    // first accounts are the Pyth oracles
    let BTC_account_info = next_account_info(account_info_iter)?;

    // check the accounts match what we expect
    if  BTC_account_info.key != &BTC_key
    {
        return Err(ProgramError::InvalidAccountData);
    }

The first thing we need to do is to just check that the account that has been passed to the program is indeed the Pyth Bitcoin account. This stops malicious individuals sending the wrong accounts, and providing fake data to our program which would give them control over the seeds generated.

    // in processor.rs 
    // get the price and confidence interval from Pyth
    let btc_price_feed = load_price_feed_from_account_info( &BTC_account_info ).unwrap();
    let btc_price_struct = btc_price_feed.get_current_price().unwrap();

From there obtaining the current price, and the confidence interval on it is incredibly straight forward, requiring only a couple of function calls to the Pyth API: load_price_feed_from_account_info and get_current_price. The btc_price_struct object has the following fields:

    pub struct Price {
        pub price: i64,
        pub conf: u64,
        pub expo: i32,
    }

and if you are actually interested in the price then it is just given by $P=(\mathrm{price}\pm \mathrm{conf})\times {10}^{\mathrm{expo}}$ , but in our case we just take the price and conf fields, and convert the price to a u64. This is safe for cryptocurrency prices, but be aware that for derivatives you may need to be more careful as prices can go negative.

    // in processor.rs 
    // the price is an i64, so first convert to a u64
    // for currencies this should be fine, but if you want a derivatives time series bear in mind that can go negative
    let btc_price_value = u64::try_from(btc_price_struct.price).unwrap();
    let btc_price_error = btc_price_struct.conf;

Using Prices To Build Our Seed Value

In our program we define a SeedStruct type which is just a vector of nine unsigned 64bit integers (u64s):

    // in state.rs
    pub struct SeedStruct {
        pub seed_prices : [u64;  9]
    }

This is because for each of our streams we are going to create three u64 values using a combination of the BTC price $\pm$ the confidence interval. We also make use of the Xorshift* RNG from the previous post, which takes a u64 as input and generates a random u64 from it. While it is probably only necessary to apply this once per input we do so twice simply to make sure we have moved further from the starting point in state space. By applying the Xorshift* generator at this point we guarantee that any delta in the price or confidence interval will yield significantly different inputs to the hashing function that will actually produce the seed.

    // in processor.rs 
    let mut seed_values = SeedStruct { seed_prices : [0; 9] };
    seed_values.seed_prices[0] = Self::shift_seed(Self::shift_seed(btc_price_value + btc_price_error));
    seed_values.seed_prices[1] = Self::shift_seed(Self::shift_seed(btc_price_value));
    seed_values.seed_prices[2] = Self::shift_seed(Self::shift_seed(btc_price_value - btc_price_error));

The final hashing step is shown below, where we make use of the fast murmur3 method described in the previous post to hash our struct into a single unsigned 128bit integer (u128).

    // in processor.rs 
    let mut vec_to_hash = unsafe{Self::any_as_u8_slice(&seed_values)};
    let h = murmur3_x64_128(&mut vec_to_hash, 0).unwrap();

    // we can take our 128bit number and get two 64bit values
    let lower  = u64::try_from(h & 0xFFFFFFFFFFFFFFFF).unwrap();
    let upper  = u64::try_from((h >> 64) & 0xFFFFFFFFFFFFFFFF).unwrap();

    let seed = lower ^ upper;
    let seed_double = Self::generate_random_f64(seed);

Whereas previously we split this u128 into two halves in order to have two independent u64 random values to use in our generator, in this case we combine them using the bitwise XOR function to produce a single u64 value as our final seed. For the purposes of this post we then also convert that to a floating point value in the range[0..1) so that we can more easily compute some statistics on it to compare to the expected uniform distribution.

Checking The Statistical Properties Of The Seed Values

Now that we have our program we can take a look at the statistical properties of the seeds we generate. Below is a javascript API that can access our on-chain program. When you click Generate Seed it will go and get the current prices for BTC, ETH and SOL and produce the seed either in the way we have described above (the 'ShiftMurmur' option) or simply by hashing the nine price values directly using a SHA256 hash function, and taking the lower 64bits as our seed. The None option simply allows you to check the baseline computation cost for everything except the process of generating the seed once the price data has been obtained.

The baseline cost of running the program is about 32000 units, of which only 5000 is actually getting the price data, the rest is spent checking that the keys are the ones that we expect. This means that the ShiftMurmur approach costs only 3000 compute units to generate the seed, compared to 18000 for the SHA256 hash. Although it seems like the process of using the Xorshift* and Murmur3 hash functions is a lot of trouble compared to a single call to SHA256, it is still the much cheaper option, at least for the number of streams we are dealing with in this example, and both will yield very different seed values for even a tiny change in the input.

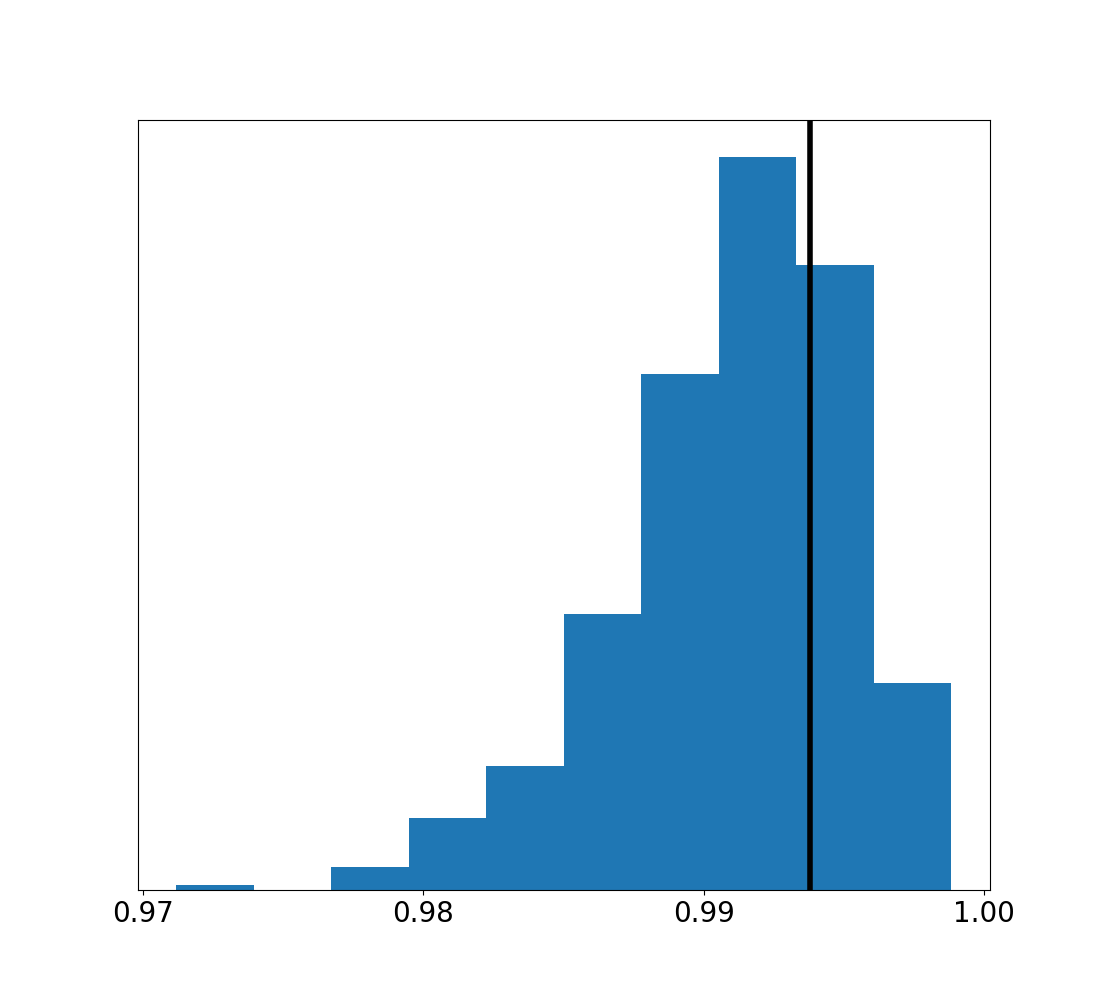
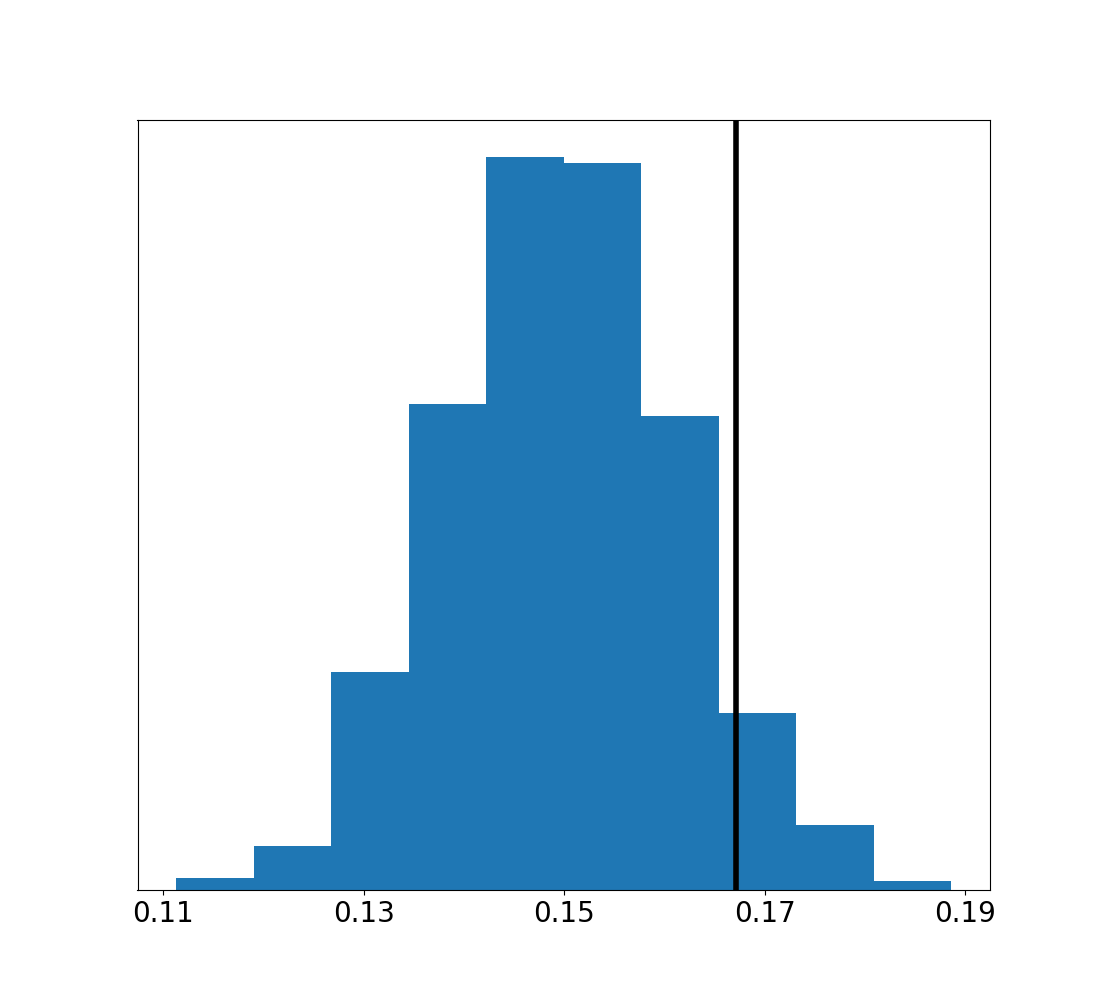
In order to get some idea of how well distributed these seeds are we computed 5000 values in a row and calculated the entropy of the histogram of those values. We then did the same thing using the Numpy uniform random number generator for one thousand realizations, in order to build a distribution of the expected entropies for a dataset of this size. We then repeated this process, but taking the absolute values of the deltas between subsequent seed values, rather than the values themselves. The images above show the entropy distributions generated using Numpy, with the vertical lines the entropy of our random seeds. Both are consistent with the Numpy RNG, and if you want to try other statistical tests you can find both the python script and the seed values that were used here in the git repository for this example.

On that note we will bring this post to a close, many thanks to Zantetsu | Shinobi Systems on the Solana Tech discord for helpful discussions on this topic. Hopefully you've learnt something about how to use Pyth to create seeds for your random number generators, and if you did find this useful or informative feel free to follow us on Twitter to keep up to date with future posts, and the release of our first proper Solana DApp!