Intro to Reinforcement Learning From Human Feedback (part 1)

October 21 2023

Introduction

Over the last few years Deep Reinforcement Learning (RL) has made remarkable progress in being applied to ever more complex environments, from Go, DOTA2 and StarCraft II, up to more recent developments in open ended games like Minecraft. Broadly speaking the RL learning loop involves an agent operating in some environment, making observations and taking actions. Some actions may result in a reward (positive or negative), for example winning a game, and the agent learns a policy for taking moves in order to maximise its long term reward.

For many interesting applications, however, encoding how the environment should hand out rewards and penalities (the reward function) is extremely challenging, and attempts to hard code this has yielded many examples of misaligment between what the agent ends up doing, and what the human designer intended.

One potential avenue that attempts to solve this problem is Deep Reinforcement Learning From Human Feedback (RLHF). In their paper (henceforth C17) the authors augment the RL process by having humans watch pairs of videos that show the agent behaving in different ways, and provide their preferences for which video is closer to displaying the behaviour desired from the problem. From these preferences a reward function is trained using a supervised learning process, and that trained reward function can then used as part of the RL process instead of relying on a hand coded function. In the paper the authors use this approach to train an agent to play atari games, and simulate robot locomotion, such as making a Hopper robot do backflips:


This could be achieved with relatively little human input, and resulted in much better behaviour than their attempt to hard code a reward function.

Since then RLHF has been used to great effect to produce fine tuned large language models such as InstructGPT, and has been a significant factor in making ChatGPT so successfull. You can find articles out there that go through the details of how to implement RLHF in this kind of context.

In this post we will take a bottom up approach, introducing some of the core concepts from RLHF, and applying them to a much simpler problem, the moving-dot gym environment. This problem simply involves a dot that is spawned at a random location in a 2D space, and must move towards the center of the screen. A single episode lasts for 2000 timesteps, during which time the environment provides a score of +1 if the agent moves closer to the center, and -1 if the agent moves further away.


By using this problem we can greatly simplify many of the details presented in the C17 RLHF implementation, but still cover the core points. In particular we will generate a database of preferences, use that database to train a reward model, and use that model to provide rewards when training the RL agent. In subsequent posts we will expand upon this basic implementation, building towards a setup that lets the user provide feedback in the atari game-playing context.

The code that we will describe can be found in our GitHub repo for this post here.

The rest of the post will be organised as follows:

• Some technical background on the RLHF implementation

• Generating the preferences database

• Training a reward model using those preferences

• Training our moving dot agent given the reward model

Some Background

Although we don't want to get too much into the weeds of the technical background that frames RLHF, there are some definitions and terminology from C17 that will be usefull in this post.

First, if we denote the ith observation of a particular environment as $o_i$, and the action taken as a result of making that observation as $a_i$, we can write a sequence of k observation-action pairs, a trajectory segment, as $\sigma =(o_0,a_0),(o_1,a_1),\dots ,(o_{k-1},a_{k-1})$.

In C17 humans were asked to compare two such segments, which we will refer to as ${\sigma }_1$ and ${\sigma }_2$, and to simply record either which segment they prefer, that they have no preference, or that they are unable to compare the two segments. These opinions are then stored in a database and used to train a reward model using supervised learning. In particular, if we write the total reward for trajectory segment ${\sigma }_1$ as $R_1=r(o_0,a_0)+r(o_1,a_1)+\cdots +r(o_{k-1},a_{k-1})$, then if the user prefers sequence ${\sigma }_1$ to sequence ${\sigma }_2$, written as ${\sigma }_1\succ {\sigma }_2$, then we want to have $R_1>R_2$.

When training the reward model, under the assumption that the human's probability of preferring a segment depends exponentially on the value of the total reward for that segment, we can write human's probability of preferring segment one as:

$P[{\sigma }^1\succ {\sigma }^2]\equiv P_1=\frac{\exp (R_1)}{\exp (R_1)+\exp (R_2)}$
From this the cross-entropy loss that describes the difference between the predictions and the actual distribution provided by the human labels is given by:

$\mathrm{loss}(r)=-({\mu }_1\log (P_1)+{\mu }_2\log (P_2)),$
where ${\mu }_1$ and ${\mu }_2$ are the actual probability distribution over the two sequences, indicating which segment was preferred by the human. This can be [1, 0] if the first segment is preferred, [0, 1] if the second segment is preferred, or [0.5, 0.5] if there is no preference.

Generating Preferences

One of the advantages of using the simple moving-dot environment is that preferences can be determined using trajectory segments that contain only single observation-action pairs. For any pair of segments we can also use a simple heuristic to determine preferences: that whichever action caused the dot to move closer to the center is preferred, and if the distance closed is the same they are ranked equally. This means that we also don't need to bother with actually implementing the human feedback bit just yet, which saves adding a significant amount of complexity to the user interface, and doesn't really impact our ability to learn what is going on.

Another nice bonus from working with such a simple problem is that we don't even need to use the gym environment to generate the preferences database. In total there are five actions that we can take, the null action (do nothing), or moving up, down, left or right. The code for this subsection is in make_preferences_db.py. We create a simple dictionary that maps the index of each action with the movement direction in cartesian coordinates of the pixel.

    
    n_actions = 5
    actions = {}
    actions[0] = np.array([0,0])
    actions[1] = np.array([0,1])
    actions[2] = np.array([1,0])
    actions[3] = np.array([0,-1])
    actions[4] = np.array([-1,0])

We can then generate a set of random positions, and actions and save these pairs in a list.

    # for some reason the gym environment can only go between (4,4) and (205, 155)
    y_min = 4
    x_min = 4
    y_max = 205
    x_max = 155

    n_segments = 10000
    segments = []
    for i in range(n_segments):
        
        obs = np.array([np.random.randint(y_min, y_max+1), np.random.randint(x_min, x_max+1)])
        a = np.random.randint(0, n_actions)
        segments.append((obs, a))

Our database of preferences can then be generated by comparing random pairs of segments using our heuristic described previously. Note that in C17 pairs of segments were chosen based on the variance of the predicted preferences using an ensemble of reward models. In our case we will just be training a single reward model and the segment pairs are just chosen randomly with a uniform distribution from the database.

    mid_point = np.array([105, 80])
    n_comparisons = 10000
    comparisons = []
    for i in range(n_comparisons):
        chosen_segments = random.sample(segments, 2)
        obs_1, action_1 = chosen_segments[0]
        obs_2, action_2 = chosen_segments[1]

        next_obs_1 = obs_1 + actions[action_1]
        next_obs_2 = obs_2 + actions[action_2]

        move_1 = np.sqrt(np.sum((obs_1 - mid_point)**2)) - np.sqrt(np.sum((next_obs_1 - mid_point)**2))
        move_2 = np.sqrt(np.sum((obs_2 - mid_point)**2)) - np.sqrt(np.sum((next_obs_2 - mid_point)**2))

        mu_1 = 0.5
        mu_2 = 0.5

        # move 1 has got closer to the center than move 2
        if (move_1 > move_2):
            mu_1 = 1
            mu_2 = 0
        
        # move 2 has got closer to the center than move 1
        if (move_2 > move_1):
            mu_1 = 0
            mu_2 = 1

        entry = [len(comparisons), int(obs_1[0]), int(obs_1[1]), int(action_1), int(obs_2[0]), int(obs_2[1]), int(action_2), mu_1, mu_2]
        comparisons.append(entry)

Each row of the database therefore contains an index, the two segments, and the distribution over the preference. When training the reward model we will sample from this database. The code for handling the database is in db.py, which we won't go into here but is just using standard SQL queries to store and retrieve the entries.

Learning the Reward Model

When training the reward model we will be using a simple fully-connected network with a single hidden layer with Tanh activation functions. This was chosen to match the architecture used in the original PPO implementation (see here for more details), and will be the same as we use in the A2C network for the actual training. In this case however there is only a single output value representing the reward, and the input is an observation-action pair.

As in the original PPO implementation we also initialise the network layers such that the weights use an orthogonal initialisation, where the input and hidden layer both have scale of sqrt(2), while the output layer has a scale of 1. In all layers the biases are intialised to have a value of zero.

    def layer_init(layer, std=np.sqrt(2), bias_const=0.0):
        torch.nn.init.orthogonal_(layer.weight, std)
        torch.nn.init.constant_(layer.bias, bias_const)
        return layer

    class RewardModel(nn.Module):
        def __init__(self, input_size):
            super(RewardModel, self).__init__()
            self.network = nn.Sequential(
                layer_init(nn.Linear(input_size, 64)),
                nn.Tanh(),
                layer_init(nn.Linear(64, 64)),
                nn.Tanh(),
                layer_init(nn.Linear(64, 1), std=1.0),
            )

        def get_reward(self, x):
            return self.network(x)

The loss function is then defined as in the technical background section. We pass it the two segments, and the probability distribution over the preference for those segments.

        def get_loss(self, segment1, segment2, mu1, mu2):
        
            reward_one = self.get_reward(segment1).squeeze(1)
            reward_two = self.get_reward(segment2).squeeze(1)

            e1 = torch.exp(reward_one)
            e2 = torch.exp(reward_two)

            P_pref_one = e1 / (e1 + e2)
            P_pref_two = e2 / (e1 + e2)

            loss = -(mu1 * torch.log(P_pref_one) + mu2 * torch.log(P_pref_two))

            return loss

To train the network we use the Adam optimizer, again taking the default settings from the original PPO implementation, and iterate over 100000 training epochs, taking a batch size of 128 random rows from our preferences table.

    reward_model = RewardModel(2 + 1).to(device)
    optimizer = optim.Adam(reward_model.parameters(), lr=2.5e-4, eps=1e-5)

    batch_size = 128
    n_epochs = 100000
    for epoch in range(n_epochs):

        entries = np.random.choice(len(preference_table), batch_size, False)
        batch = preference_table[entries]
        s1 = torch.tensor(batch[:,1:4], dtype = torch.float).to(device)
        s2 = torch.tensor(batch[:,4:7], dtype = torch.float).to(device)
        m1 = torch.tensor(batch[:,7], dtype = torch.float).to(device)
        m2 = torch.tensor(batch[:,8], dtype = torch.float).to(device)

        loss = reward_model.get_loss(s1, s2, m1, m2).sum()
        
        optimizer.zero_grad()
        loss.backward()
        optimizer.step()

Below we show a moving average of the training loss, averaged over the last 100 epochs. After 100000 training epochs the training loss has pretty much flattened out. Possibly we could train for longer to improve this slightly but for our purposes this is probably sufficient.



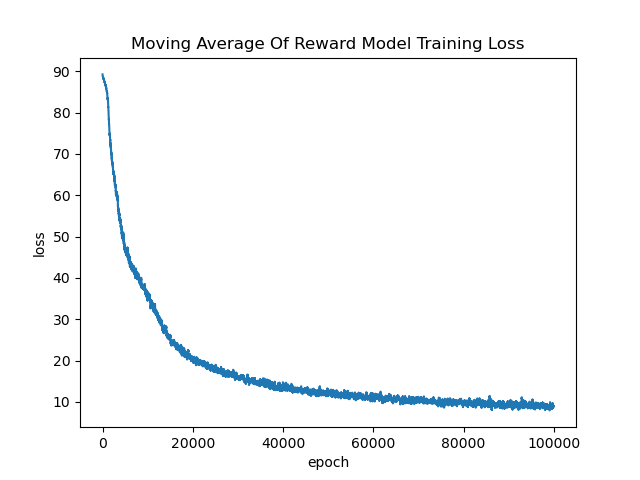
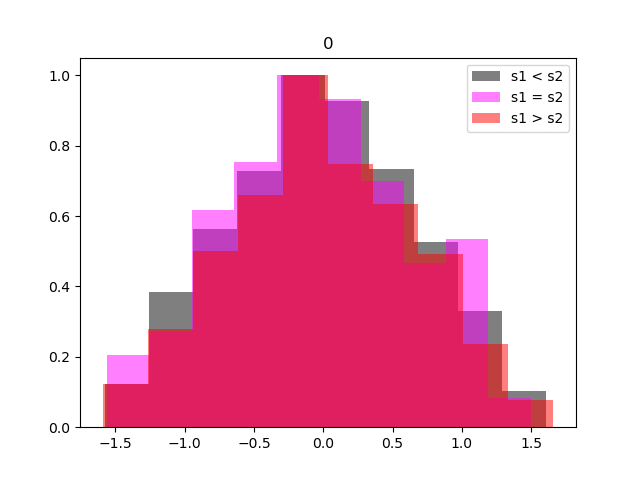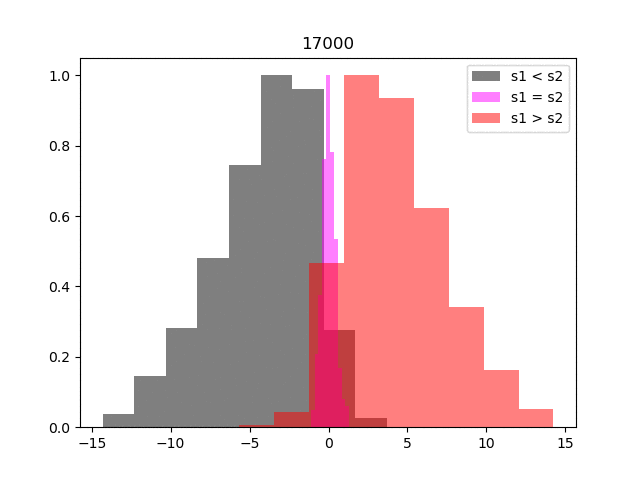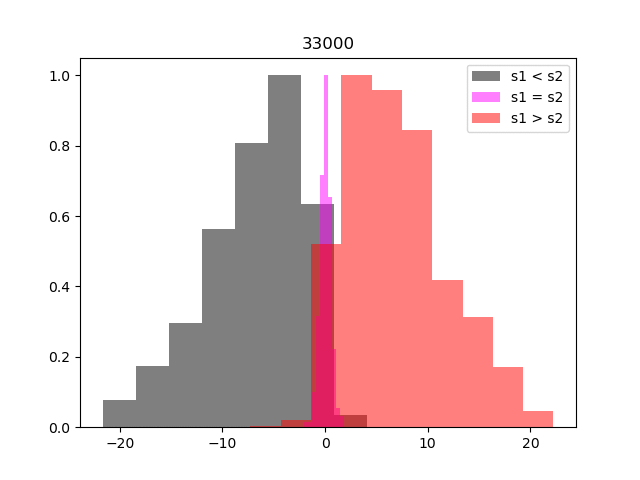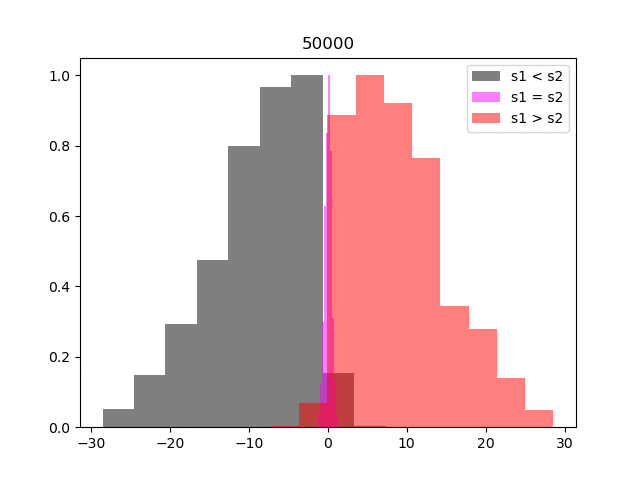
Below we illustrate the progress of the training by testing how well the reward model is able to reflect the preferences. At regular intervals we take the entire preference table, and split the entries into three groups, where segment one is preferred, segment two is preferred and where there is no preference. We calculate the reward for each segment and then histogram $R_1-R_2$. If the reward model is working, then $R_1$ should be greater than $R_2$ when segment one is preferred, and so those points should all have positive values. Similarly when segment two is preferred those points should all have negative values, and when there is no preference those points should be clustered around zero.

Within relatively few iterations the network has learnt to represent the preferences accurately, so we can move on to training our agent.

Training the RL Agent

To train our agent to play the moving dot game we start with an implementation of an A2C network using PPO, which you can find here. It uses a seperate network for the agent and the critic, each of which has the same design as in our reward model. We won't go into the details of this file in this post, but will simply describe how to use the reward network trained previously in place of the standard reward provided by the gym environment.

Firstly we add an extra argument that the user can pass --rlhf which will initialize the reward_network from the file saved in the previous step. It then sets the network to eval mode as we won't be doing any updating of the weights from this point.

    reward_network = None
    if (args.rlhf):
        reward_network = RewardModel(2 + 1).to(device)
        reward_network.load_state_dict(torch.load("./rewards_model"))
        reward_network.eval()

Then all we need to do is to pass the observation-action pair to the reward model to calculate the reward, and overwrite the original reward produced by the gym environment, everything else in this file remains exactly the same. Note that as in C17 we are clipping the reward to a range of +/- 1.

    # if we are using RLHF then we want to replace the reward with the value from the reward network
    if (args.rlhf):
        for i in range(len(reward)):
            reward_input = torch.tensor([new_obs[i][0], new_obs[i][1], action[i]], dtype=torch.float).to(device)
            raw_reward = reward_network.get_reward(reward_input)
            clipped_reward = torch.clamp(raw_reward, -1, 1)
            reward[i] = clipped_reward

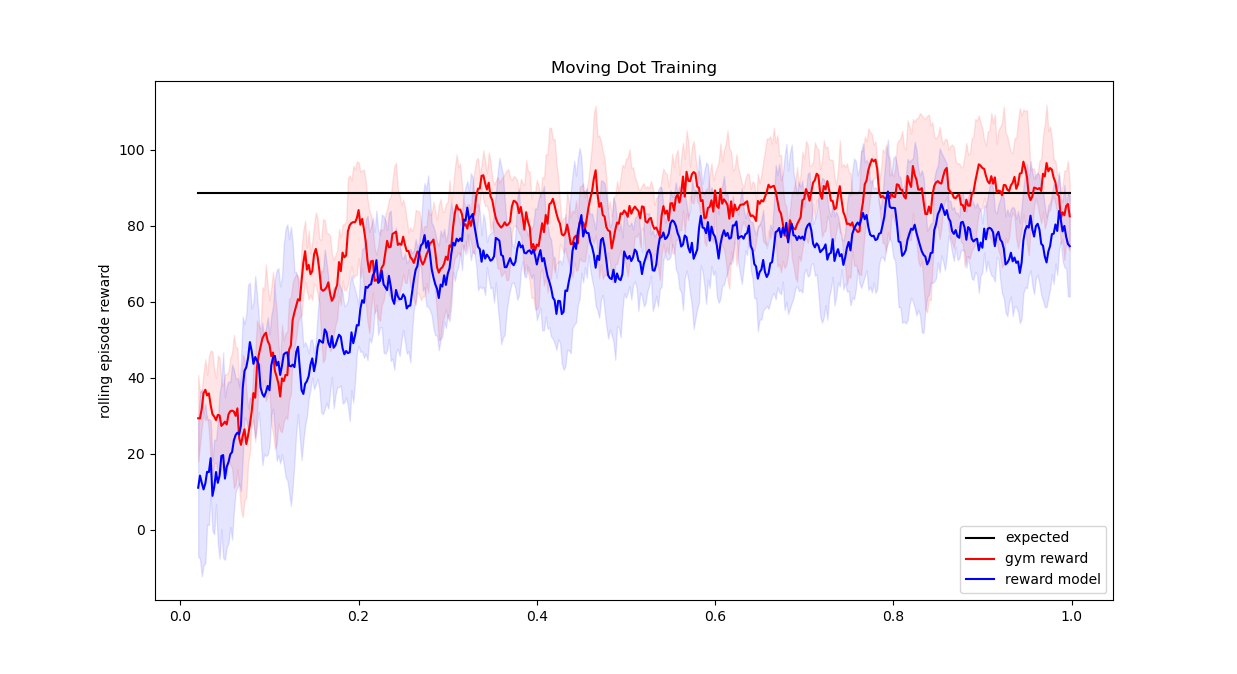
We run this process for 1000000 timesteps, with and without the additional RLHF parameter for 5 random initialisations each. The gym environment simply runs an episode for 2000 timesteps before exiting, with no opperunity to exit early. Below you can see a comparison of the mean rolling episode reward over those 5 initialisations, and the +/- 1 standard deviation window. Given the set of possible starting points we would expect this average to be roughly 88.5 assuming optimal behaviour as measured with the original gym reward. Although both are consistent with that value the network trained with the original reward is really bang on that average line whereas the network trained with the reward model comes in slightly below. This is to be expected though, and indeed in the original RLHF the goal is simply that ideally the agent will achieve reward nearly as high as if it had been using the original reward function.

And thats it! We hope that you have found this post informative, we will be following it up with more complex examples using RLHF. In particular next time we will use a gym environment that requires us to train our reward model on segments made up of a sequence of states, rather than just individual ones, and will start to implement some of the additional bells and whistles from the full implementation. If you did find this post useful go ahead and follow us on X to keep up to date with future posts!